Using Feedback With Student Centered Instruction

Let’s take a closer look at the rubric I use for addition with regrouping.

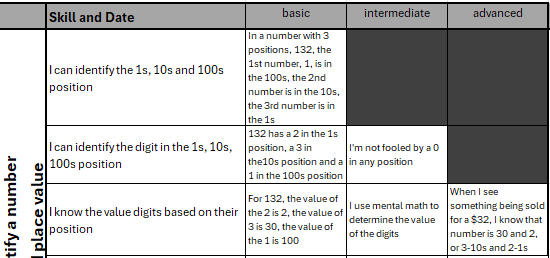
An examination of this rubric reveals that the foundational skills of identifying digits, the position and the place value of those digits are integrated into the instruction. This is a central part of skill development for regrouping. 

I developed this rubric based on my experience with students who struggle with this skill. The influence from Standards Mastery and Building Thinking Classrooms is visible in this rubric. The specific skills listed are in student friendly language and refer to a specific standard and objective in the math common core. For each objective, I added a problem I expect students to solve accurately to be considered proficient for that objective.  Each problem also defines the levels of basic, intermediate and advanced for each objective unless the skills are considered a basic or intermediate level skill. In that case, the skill level that does not apply is blacked out. The result is that students and the teacher are able to use the feedback from the rubric to track students’ progress on the standard.

When I used an earlier version of this rubric with students, I paired it with games I created to introduce new skills and build fluency with those skills. When students struggled with the concept of bundling and unbundling, I used a game that required students to bundle and unbundle tens and ones or tens and hundreds. When students struggled with decomposing a number, I used a card game that required that students match different representations of the same number. The games not only helped students understand the foundational skills, they also helped build procedural knowledge that helped students demonstrate proficiency when given actual problems to solve.

It is important to note that while the rubric is built with the different skills in a specific order, it is not necessary to strictly follow that order. For example, I introduce bundling and unbundling with a game before I start instruction on regrouping. I also had students practice bundling and unbundling on addition problems without regrouping to introduce the strategy, build the foundational skill and the flexible thinking needed to represent the same number in different ways, such as expanded form.

When I introduced regrouping with addition, students were able to break down numbers by place value, reorganize the tens and ones, and compose the new number as a sum of its addends. Students were always started at the most basic level, in this case a 1-digit number added to a 2-digit number. They used the skills they developed through games, previous instruction and practice to solve increasingly difficult problems.

This student centered approach to instruction had the added effect of changing students’ beliefs in what they are able to do, that they can solve difficult math problems. Best of all, students did not shut down when given addition with regrouping problems with larger numbers and multiple points to regroup.

It is possible to see how this instructional method and rubric can blend easily with success criteria and essential questions.  However, that is something I’ll save for the next blog post. 

© 2025 Linda Patrell-Kim

If you have questions or comments, please share.